What is the Best Simple Way to Explain Permutations and Combinations?

Permutation and combination are the important statistical concepts which are used for getting number of possible rearrangements and also choosing some from larger set of elements. Here we will study briefly about permutation and combination and along with that we will figure out the best possible way to simplify its significance and applications. Before that we first deduce what exactly permutation and combination is and what is the fundamental difference between these two. Basically, permutation and combination are used as methods for determining and computing the possible outcomes in various scenarios. In simple terms we can say that permutations are considered as arrangements where order does matter where combinations are understood as selections where order does not matter.
Suppose there are 17 men and 9 women in the management team of a company. If a man or a woman has to be selected as a managing director of the company, the CEO has an option of either selecting 1 out 17 men or selecting 1 out of 9 women. Thus, they have total of 17+9=25 ways i.e., the sum rule of counting. Let us consider a different scenario where a person has 3 pants and 5 shirts. And every day he wears a different set of pant and shirt. Now there are many possible ways through which he can wear the dress. One would be wearing a separate colour pant with separate colour shirt and other day with different colour shirt. So, he has 3 pants choices and 5 shirt choices. Thus, a total combination of 3*5=15. Therefore, the person can try 15 combinations using product rule of counting.
For having a understanding permutation and combination a term factorial has to be known first. The factorial is nothing but a product of first n natural numbers and is denoted by n!. It is denoted as the number of ways of arranging n different objects.
Thus we can say that as of now permutation and combination are the mediums of representing a group of elements by selecting all of them in a group and forming subgroups. It is a way to define different ways to arrange a certain group of elements. Both the concepts of permutation and combination are highly important in mathematics.
For a brief illustration we will go one by one and try to derive its form in mathematical form in a simplest form.
Permutation
In simple mathematical term, it relates the arrangements of all the objects of a set into a defined order or sequence. In simple terms we can say that if the group or set is ordered, the rearrangement of the elements is called as permuting.
Combination
Combination in mathematical sense is a method of selection of elements from a large group, such that the sequence of the selection does not matter. In short, we can say that it is very much possible to count the number combinations. Combination refers to the combination of n things in which some k items are taken at a time without repeating.
However, many formulae are there in the concepts of permutation and combination in mathematics but the two most fundamental are:
Permutation formula: A permutation is the arrangement of r things from a group of n things without replacing and where the sequence of arrangement matters.
nPr = (n!) / (n-r)!
Combination Formula: A combination is the selection of r things from a group of n things with replacement and where the order of selection of elements does not matter.
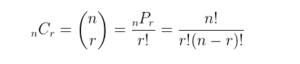
Derivation of Permutations Formula
Since a permutation involves selecting r distinct items without replacement from n items and order is important, by the fundamental counting principle, we have
P(n,r)=n.(n-1).(n-2).(n-3)……(n-(r-1)) ways.
Thiscan be written as:
P (n, r)=n.(n-1).(n-2).(n-3)….(n-r+1)————— (1)
Multiplying and Dividing (1) by (n-r) (n-r-1) (n-r-2)……….. 3. 2. 1, we get
P (n, r) =
n.(n−1).(n−2).….(n−r+1)[(n−r)(n−r−1)(n−r−2)…3.2.1][(n−r)(n−r−1)(n−r−2)….3.2.1]n.(n−1).(n−2).….(n−r+1)[(n−r)(n−r−1)(n−r−2)…3.2.1][(n−r)(n−r−1)(n−r−2)….3.2.1]
P (n, r) = n!(n−r)!n!(n−r)!
Derivation of Combinations Formula
Since combinations involve choosing r objects out of n objects where the order doesn’t matter, we can determine that:
C(n,r) = the number of permutations /number of ways to arrange r objects. [Since by the fundamental counting principle, we know that the number of ways to arrange r objects in r ways = r!]
C(n,r) = P (n, r)/ r!
C(n,r) = n!(n−r)!r!n!(n−r)!r!
Thus we derive C(n,r) =n!r!.(n−r)!
Key Differences between Permutations and combinations
- Permutations are the tools where sequence of arrangement matters.
- Combinations are used only when the number of elements are needed and the order of selection of items/elements does not matter.
- Combinations are widely used for similar kind of elements whereas permutations are used for different kind of elements.
- The permutations of two things from set of given three things, x, y, z is xy, yx, yz, zy, xz, zx.
- The combination of two things from given set of three things x, y, z is xy, yz, zx.
- For a given set of n and r values, the computed answer of permutation is found to be larger than that of combination.
Important Question: How many 4-digit numbers can be formed by using the digits 1 to 9 if repetition of digits is not allowed?
Visit for more website: wiexi.com
Visit for more website: forbesblog.org




